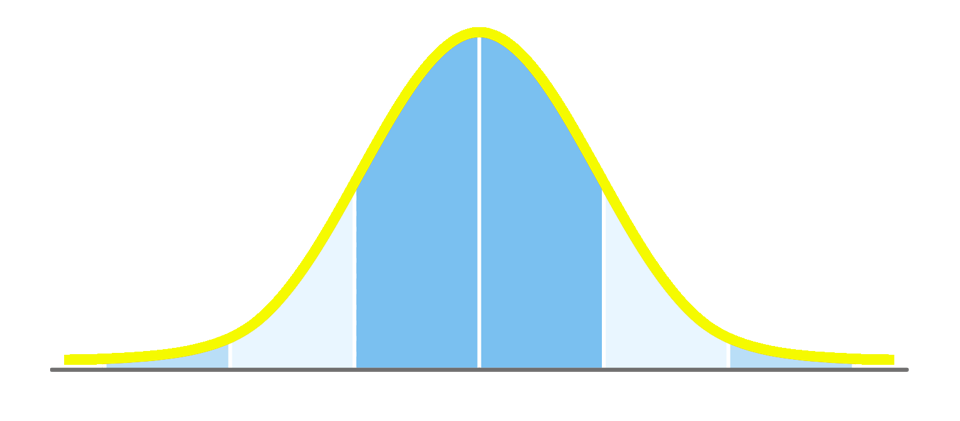
Voorbeeld 2: Examenresultaten
Je analyseert de examenresultaten van een groot aantal studenten. In een normaal verdeelde dataset scores haalt meerderheid van de studenten eens score dichtbij het gemiddelde, in dit geval een 7. Slechts een klein aantal studenten scoort uitzonderlijk hoog of laag. Als de resultaten van dit examen een standaardafwijking van 1 hebben, hebben de meeste studenten (ongeveer 68%) een score hebben tussen de 6 en 8. Een klein deel, zo’n 5% van de studenten, heeft een score onder de 5 of boven de 9.
Voorbeeld 3: Snelheid van hardopers
Bij een marathon lopen de meeste hardlopers met een snelheid van ongeveer 10 kilometer per uur. We kennen allemaal die topatleten die iets meer dan twee uur nodig hebben. Een aantal lopers zijn dus veel sneller of juist langzamer dan de gemiddelde loper.
Als je de snelheden van alle hardlopers in een grafiek zou zetten, krijg je een klokvormige curve, waarbij de meeste hardlopers zich rond de 10 km/u bevinden. Met een standaardafwijking van 1,8 km/u, loopt dus 32% van de hardlopers onder de 8,8 km/u of boven de 11,2 km/u.