In deze blog vertellen we je wat de formules bij de normale verdeling zijn, hoe de percentages werken en waarom deze belangrijk zijn.
De normale verdeling, ook wel bekend als de ‘Gaussische verdeling’ of ‘bell curve’, is een van de belangrijkste begrippen in de statistiek. Deze verdeling beschrijft hoe data zich gedraagt van onderwerpen zoals lengte, gewicht of eindexamencijfers van middelbare scholieren. De grafiek van een normale verdeling herken je aan de klokvormige grafiek. Deze klokvorm is symmetrisch met het gemiddelde als middelpunt.
De normale verdeling: een simpele uitleg!Waarom is die normale verdeling nou belangrijk? En wat heb je eraan? Om dit te begrijpen is het handig om eerst goed te snappen wat het gemiddelde en de standaarddeviatie is.
Als we als voorbeeld de meting van 1.68 pakken, bereken je de deviatie zo: d = 1.68 – 1.76 = -0.08 meter
De standaarddeviatie (symbool: s) bereken je door vervolgens alle deviaties te kwadrateren en bij elkaar op te tellen. Dan krijg je dus de som (symbool: ∑) van alle d’s: -0.08² + -0.04² + 0² + 0.03² + 0.10² = 0,027. Vervolgens deel je die door N van 5, dus: 0,027 / 5 = 0,005. Van 0,005 trek je de wortel, daarmee kom je op 0,07. Hiermee heb je (eindelijk ;)) de standaarddeviatie van jouw steekproef berekend.
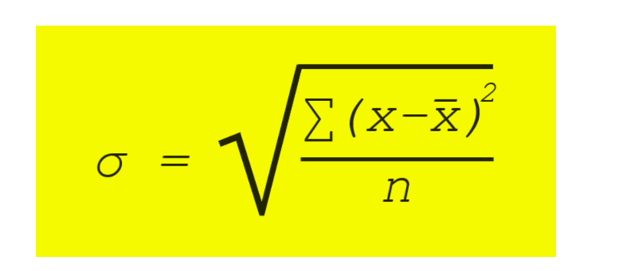
In een normale verdeling verdeelt de data zich op een voorspelbare manier rond het gemiddelde. Dit leidt tot percentages die je altijd terugziet bij de normale verdeling:
Deze percentages worden vaak samengevat in de ‘68-95-99,7 regel,’ wat een makkelijke manier is om te onthouden hoe de data verdeeld is in een normale verdeling.
Deze percentages zijn belangrijk, omdat ze je een manier geven om voorspellingen te doen en conclusies te trekken over je verzamelde data. Als je bijvoorbeeld weet dat de lengte van een groep mensen normaal verdeeld is met een gemiddelde van 1.70 m en een standaarddeviatie van 0.1 m, dan kun je met zekerheid zeggen dat 68% van de mensen tussen de 1.60 m en 1.80 m lang is.
De normale verdeling is een bekend begrip in de statistiek. Het is een voorspelbare en symmetrische verdeling van data rond het gemiddelde. De percentages (68%, 95%, en 99,7%) die binnen respectievelijk één, twee, en drie standaarddeviaties van het gemiddelde vallen, helpen je om beter te begrijpen hoe data zich spreidt. Of het nu gaat om het analyseren van lengtes, examencijfers of klanttevredenheidscijfers, veel type data is normaal verdeeld. De normale verdeling zorgt ervoor dat je de meeste statistische toetsen kan gebruiken om jouw data te onderzoeken
Aan de slag met statistiek? Volg een green belt training!
Of je nu een organisatie leidt, een project managet of je persoonlijke ontwikkeling onder de loep neemt: strategie begint met inzicht. De SWOT-analyse is al decennialang één van de meest gebruikte modellen om dat inzicht te krijgen.
Dit boek leert je niet hoe je meer doet in dezelfde tijd, maar juist hoe je keuzes maakt waardoor je minder druk bent. Aanrader!
Werken met nieuwe systemen lijkt vaak de oplossing. Maar het is slim om eerst een proces te verbeteren voor je het gaat digitaliseren.